과거에 배웠던 classification 혹은 clustering 보면 아래와 같은데,
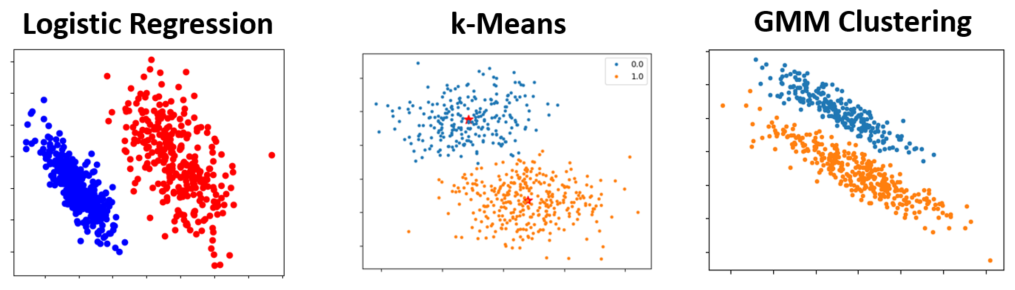
주어진 데이터를 둘 이상의 class혹은 clustering으로 “분리” 해야한다.
내부 알고리즘은 그렇지 않지만, 위와 같은 Data를 놓고 “야 얘네 둘로 분리 해봐” 하면, 가장 자연스러운 접근은 이럴 것이다
“둘을 분류하는 경계를 먼저 구하고, New data가 들어와도 경계 이 쪽에 있으면 파랑, 저 쪽에 있으면 빨강”
그럼 최적의 경계란 어찌 구하면 좋을까? Logistic regression 의 데이터 다시 보고 자연스럽게 가장 좋다고 생각한 직선 경계를 한번 그어보자.
(직선임을 다시 한번 강조)
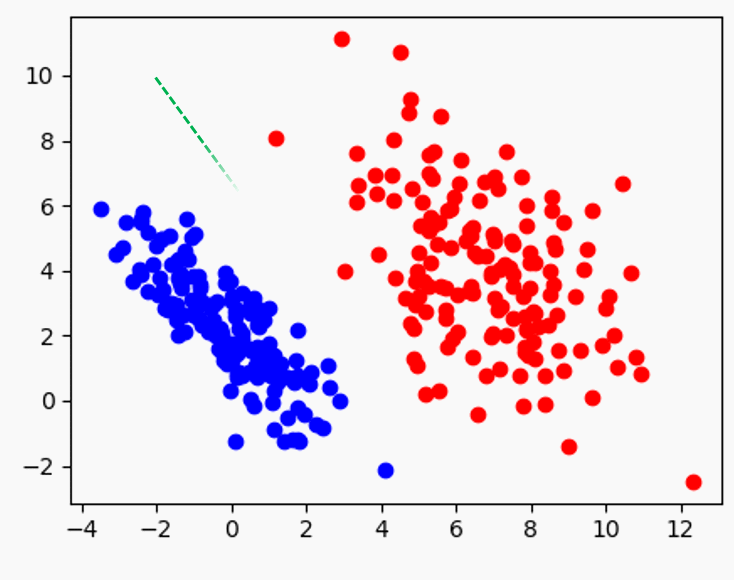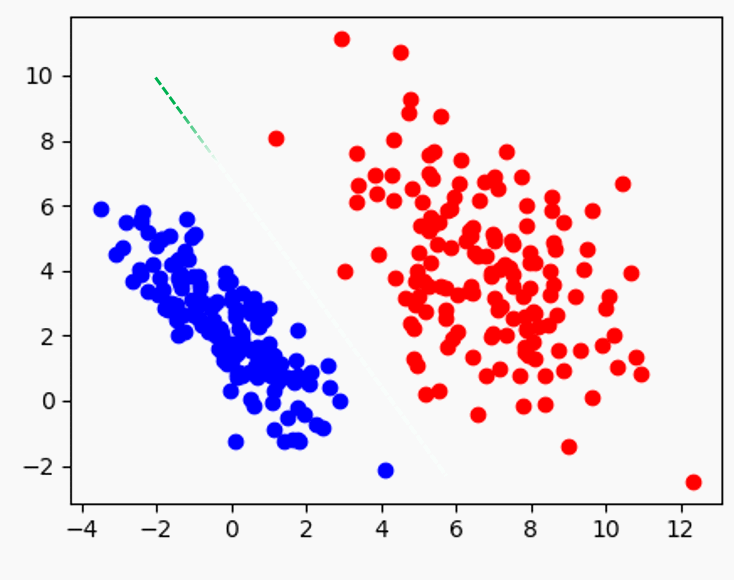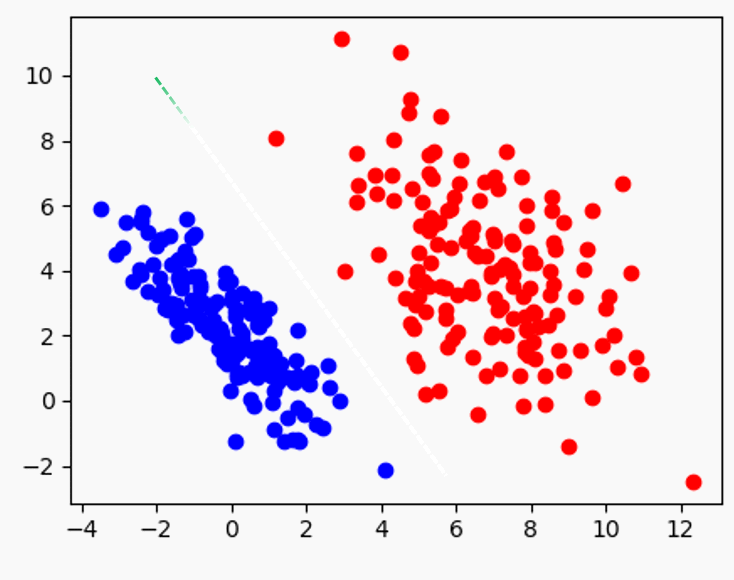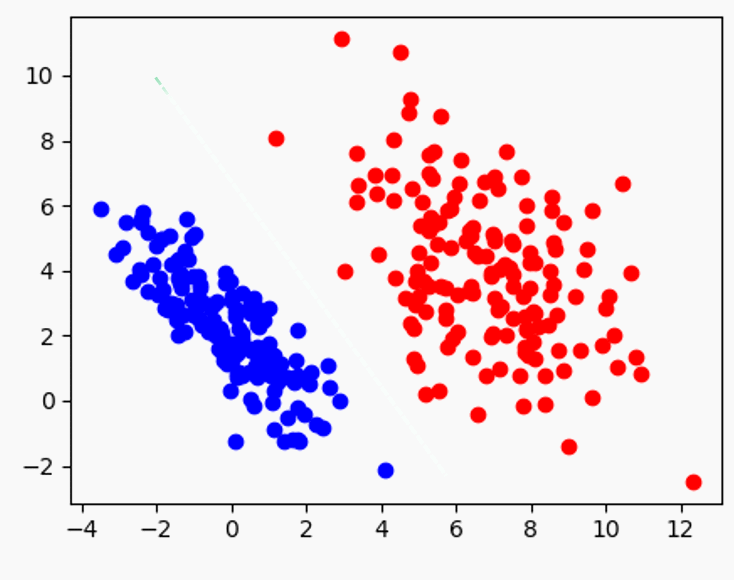
자연스럽게 생각한 바람직한 직선 경계의 조건은 뭔지 곰곰히 곱씹어보면, 아마 다음일 것이다:
1) 두 데이터의 중간에 위치하되, 2) 두 데이터 까지의 거리가 최대
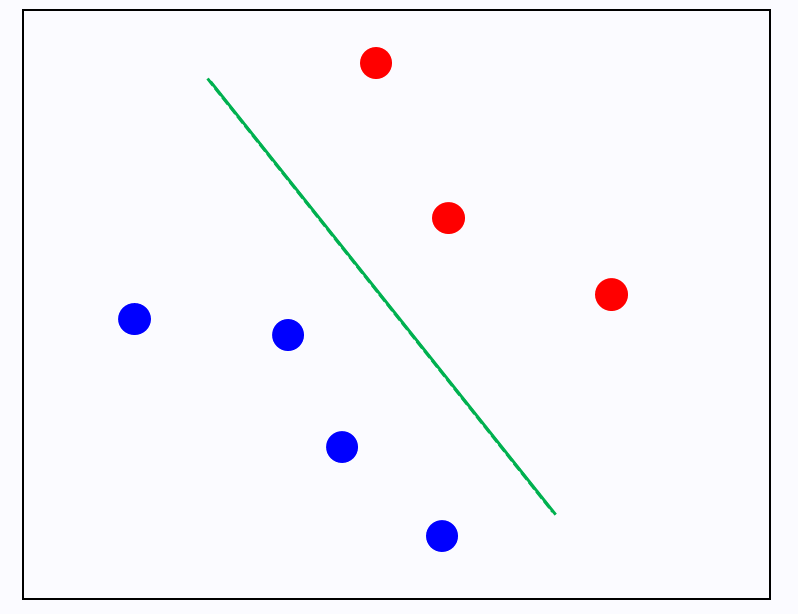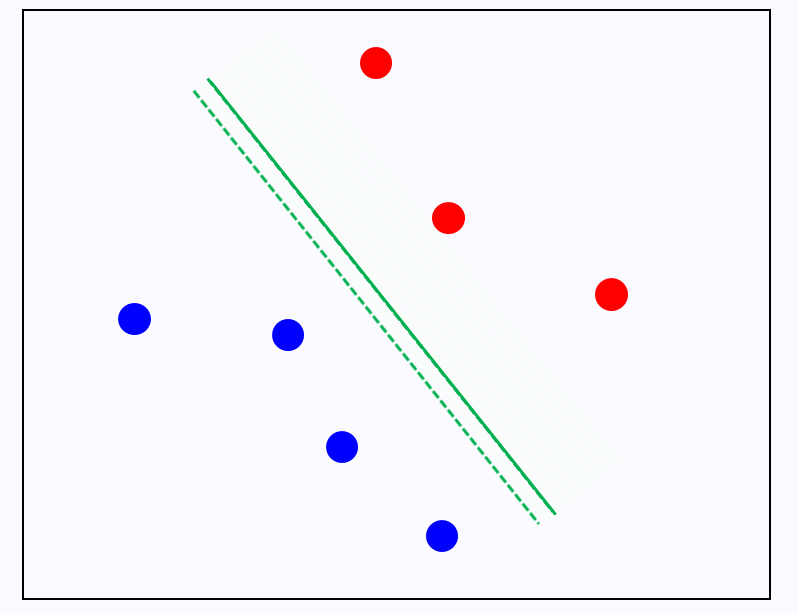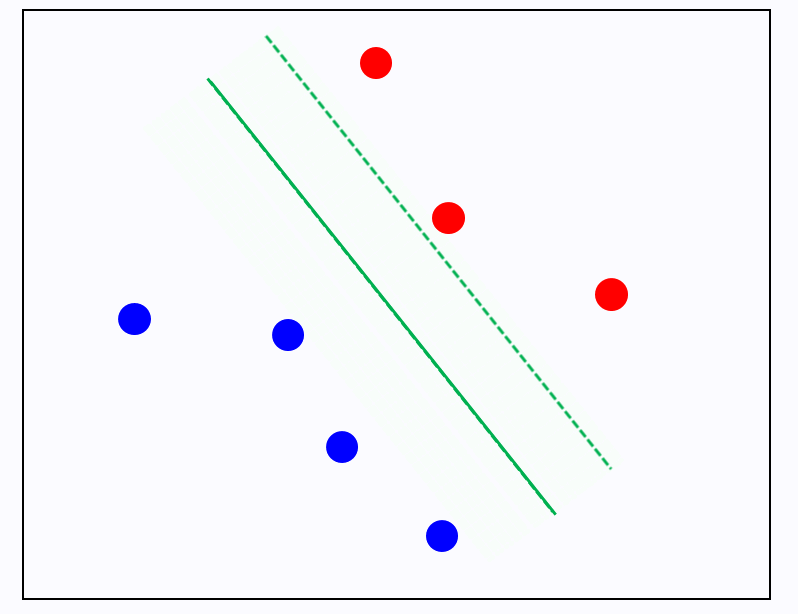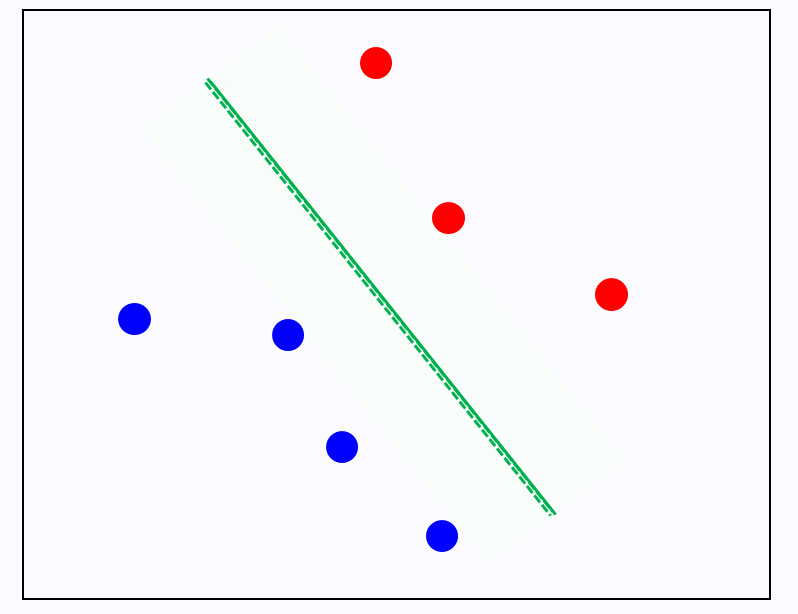
1) 이 성립 안하면 뭔데? 아래 그림에서 실선이 아닌 점선으로 경계를 결정한다는건데,
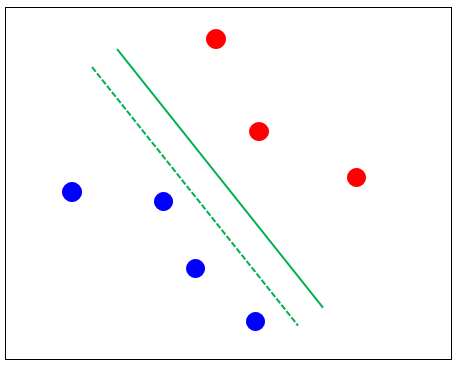
그런 경계는 아래와 같이 보라색 별 같은 data가 들어오면 빨간색으로 분류해버릴 것이다. 파란색이 합리적이여 보이는데!
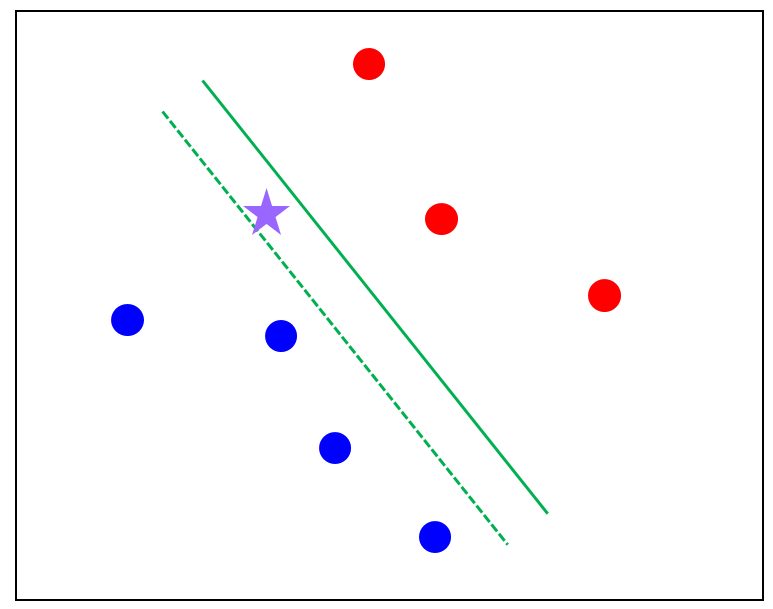
2)가 성립안하면 뭔데? 똑같이 1)이 성립하더라도 아래 그림에서 초록과 보라 중 뭘 고를건가? 보라를 골랐다면 2) 조건을 만족 안한 것이다.
보라보다는 초록 경게가 더 바람직함을 알 수 있다.
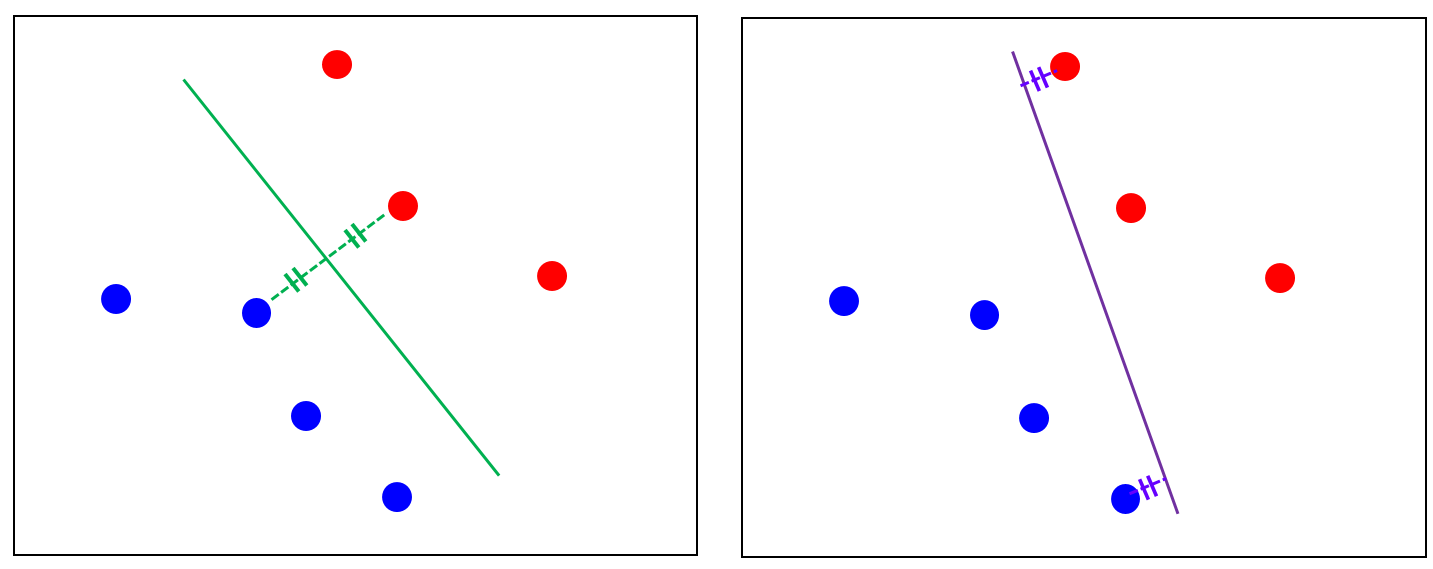
그래서 딱 1), 2) 모두 고려했을때 아래 와 같이 초록 직선으로 경계가 결정되는 것. 이는 직선이 수학적으로 2가지 조건이 있어야 결정되는 것과 일맥상통 한다
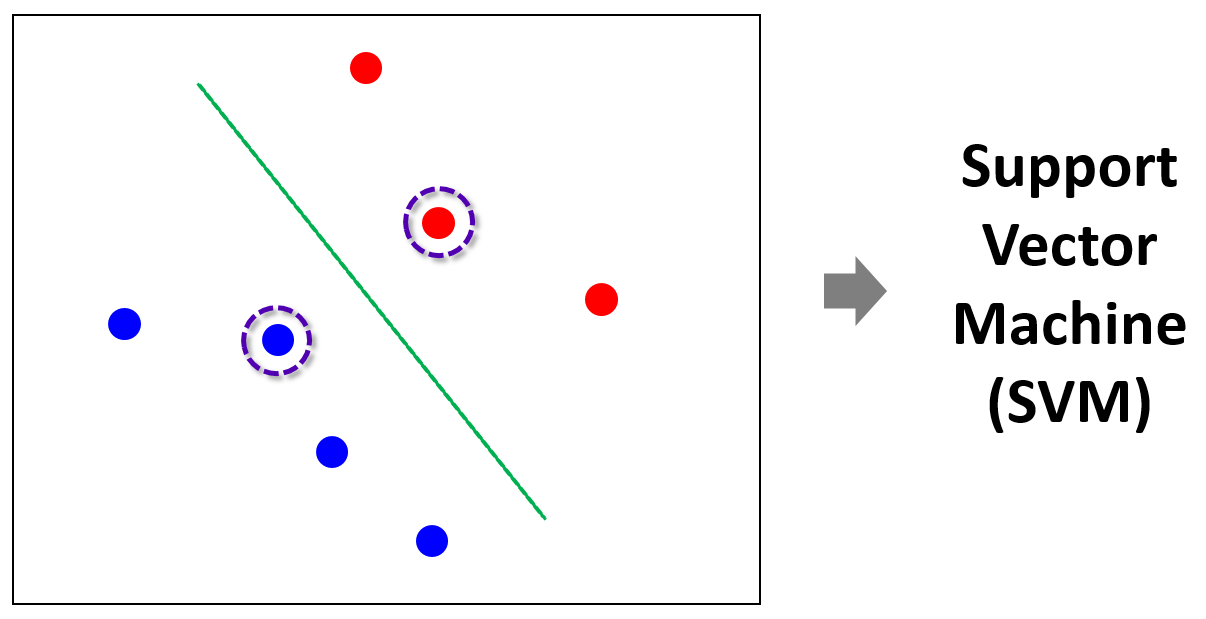
자 그럼 초록색으로 정했다고 가정 (아래 그림의 실선)하고, 여태 배운 경계 – 경계를 정하는 과정 – 데이터의 관계를 마음대로 다음 그림으로 표현 가능하다
경계가 막 움직이다가 data에 닿으면 다시 돌아가는 이상한 그림인데,
이 모양새에서 양쪽에서 두 점 (Vector)이 직선 경계를 서로 탕탕 튕겨내면서 지지 (Support) 하고 있다.
저 지지하는 두 vector를 support vector라고 하고 이러한 기준으로 경계를 결정해서 classify하는 데 사용하는 machine learning algorithm이 Support Vector Machine (SVM)이라 하며, 기본적으로 classification algorithm이다 (즉, 아래 그림에서 보라색 동그라미로 표시한 vector가 support vector임)
계속 직선 경계라고 했는데, SVM은 기본적으로 효율적이고 명료한 계산을 위하여 linear boundary를 사용함. 위에는 2차원이니까 직선이지, 3차원이면 평면이고 4차원이상이면 hyperplane임. linear boundary라는 것은 boundary가 아래와 같이 표현 가능하다는 것.
아 Linear boundary뿐이야? 그럼 아래와 같이 linearly inseparable 한 data는? 구분 못하는 것임?
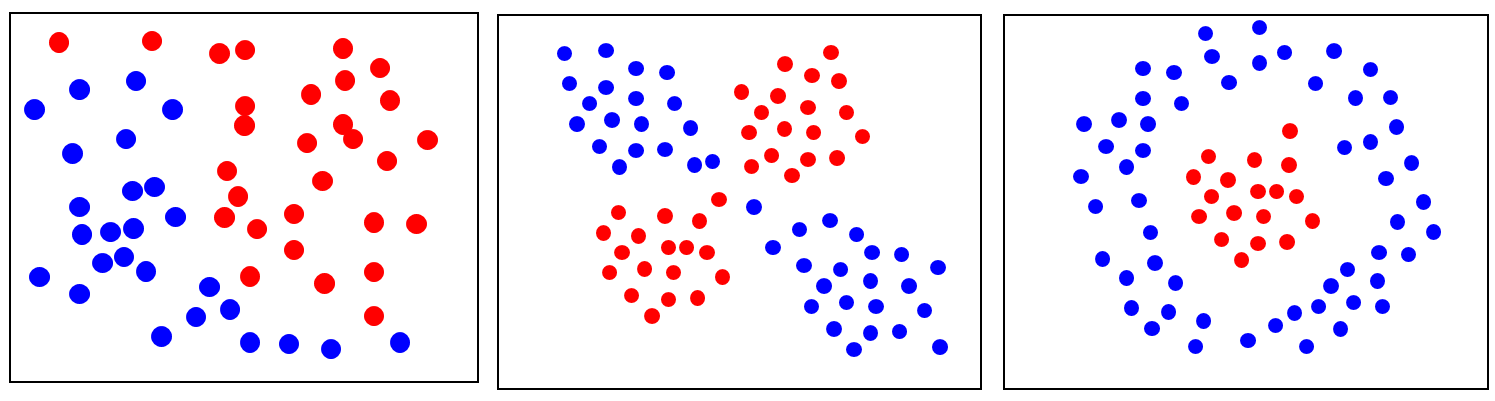
응 못해. 라고 하면 오늘날의 SVM이 없었을 것이다. 포기하지 않고 kernel trick을 SVM에 적용하여 SVM이 더 powerful해진다. 즉,
SVM에 kernel trick을 함께 이용하여 linearly inseparable data를 linear boundary로 성공적으로 분류할 수 있다.
자, 그래서 앞으로 다음순으로 SVM을 다룰 예정이다.
- SVM 배우기 위한 배경 지식
- Kernel Trick
- Lagrange multiplier
- SVM classification model 수학적 유도
- SVM에 kernel trick 적용하여 linearly inseparable data 마저 분류
- SVM + kernel trick의 python coding 연습
[끝]